Dijkstra 算法
Data Structures Experiment #13 - 完成Dijkstra算法,实现单源最短路的求法(邻接表表示)
完善给出的Graph类。
Graph(int max_v);
构造函数,max_v 是顶点的个数。~Graph();
析构函数,释放分配的空间。void addedge(int s, int t, int w);
添加一条从s到t,权重为w的有向边。int getV();
获得图中顶点的个数。int* dijkstra();
获取从1出发的单源最短路数组。如果某个点无法到达则长度为-1。
0x00 数据域封装
与#12基本相同。
增加了inDegree数组以存放各顶点入度,dij数组以存放dijkstra算法生成的单源最短路数组:dij[i]代表顶点1到顶点i的最短路权。
1 | private: |
0x01 构造函数
与前三次基本相同。
初始化dij[1]为0,其他均为-1。
1 | Graph::Graph(int max_v){ |
0x02 addedge
与#12基本相同。
1 | void Graph::addedge(int s, int t, int w){ |
0x03 getV
判断出度和入度不同时为零。
1 | int Graph::getV(){ |
0x04 dijkstra
设顶点数为count,则至多只需count-1次(即left次)更新dij数组即可。
更新前的准备工作:
声明每次更新时从
dij数组找到的未访问过的最小值以及它的下标,visit数组用于判断是否访问过此顶点,并将dij数组初始化(类似广度第一层)。开始更新:
先初始化
min,找一个未访问过的且距离不为无穷的顶点。若找完后i > count,则说明没有符合条件的顶点,即未访问过的顶点都是无穷远的顶点,说明算法已经结束,直接break。初始化后,再逐个比较找到最小值,并更新最小值及其下标。成功找到最小值后将该顶点记为已访问。
从最小值顶点开始遍历其链表,设指针为
p,判断1->(不一定直达)->min_index->p->dest路径总权(p->cost+min)是否比1->(不一定直达)->p->dest(dij[p->dest])小,取较小者更新dij[p->dest]。
更新后:
观察
main.cpp,发现要求dijkstra算法生成的单源最短路数组为从0开始,则只需将dij数组整体前移1位。释放内存并返回。
完整算法如下。
1 | int* Graph::dijkstra(){ |
0x05 析构函数
逐结点释放内存。
若main.cpp末尾有以下语句:
1 | delete arr; |
则无需在析构函数中释放dij数组内存。
1 | Graph::~Graph(){ |
0x06 补充
建议增加测试样例,现提供一个如下(供参考)。
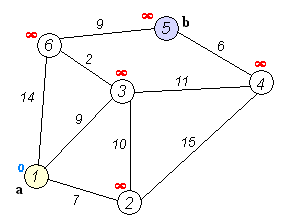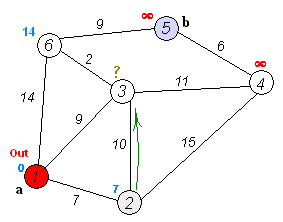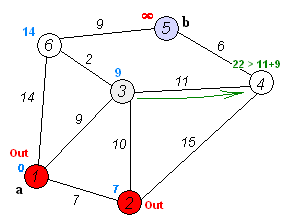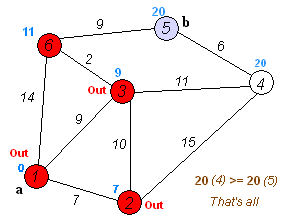
1 | Graph g1(7); |