位运算实验（下）

发表于 2020-04-11 分类于技术阅读次数：本文字数： 1.8k 阅读时长 ≈ 6 分钟

Data Lab: Manipulating Bits #2 - 对于实验一（Data Lab）的一些想法（下）。

这个实验要求学生实现简单的逻辑和算术运算函数，但是只能使用一个非常有限的C语言子集。比如，只能用位级操作来计算一个数字的绝对值。这个实验可帮助学生了解 C语言数据类型的位级表示，以及数据操作的位级行为。

Puzzle 1 - conditional

conditional - same as x ? y : z
Example: conditional(2,4,5) = 4
Legal ops: ! ~ & ^ | + << >>
Max ops: 16
Rating: 3

利用位操作来实现三目运算符表达式x ? y : z的功能，只需判断x是否为0：若不为0则返回y；反之则返回z。

同样可以利用算术右移的特点制作一个掩码（mask），类似#1中提到的“模版”，以便于操作。

int conditional(int x, int y, int z)
{
    int msk = (!!x) << 31 >> 31;
    return (msk & y) | (~msk & z);
}

Puzzle 2 - isNonNegative

isNonNegative - return 1 if x >= 0, return 0 otherwise
Example: isNonNegative(-1) = 0. isNonNegative(0) = 1.
Legal ops: ! ~ & ^ | + << >>
Max ops: 6
Rating: 3

判断符号位即可。

int isNonNegative(int x)
{
    return !(x >> 31);
}

Puzzle 3 - isGreater

isGreater - if x > y then return 1, else return 0
Example: isGreater(4,5) = 0, isGreater(5,4) = 1
Legal ops: ! ~ & ^ | + << >>
Max ops: 24
Rating: 3

比较大小，显然当x为正且y为负时，一定有x > y成立；当x为负且y为正时，上式一定不成立。

当x与y同号时，判断二者之差是否为正即可。注意题目要求，当二者相等时返回0，故此处作差时减1。

判断正负依然利用符号位。

int isGreater(int x, int y)
{
    int _x, _y, sub;
    _x = x >> 31;
    _y = y >> 31;
    sub = (x + ~y) >> 31;
    return (!_x & _y) | (!(_x ^ _y) & !sub);
}

Puzzle 4 - absVal

absVal - absolute value of x
Example: absVal(-1) = 1.
You may assume -TMax <= x <= TMax
Legal ops: ! ~ & ^ | + << >>
Max ops: 10
Rating: 4

正数的绝对值为其本身，负数的绝对值为其相反数。

位全0取反为-1（~0 + 1 = 0），全1取反为0。

依然可以利用符号位右移作为掩码，当x为正时掩码全0，异或后仍为原值；当x为负时掩码全1，异或后相当于取反的效果，再加1即得到其相反数。

int absVal(int x)
{
    int _x = x >> 31;
    return (x ^ _x) + (~_x + 1);
}

Puzzle 5 - isPower2

isPower2 - returns 1 if x is a power of 2, and 0 otherwise
Examples: isPower2(5) = 0, isPower2(8) = 1, isPower2(0) = 0
Note that no negative number is a power of 2.
Legal ops: ! ~ & ^ | + << >>
Max ops: 20
Rating: 4

一个数为2的幂次，即其二进制位有且仅有1位为1。

不妨设其中1所在最低位为第n位，则减1后其0～n-1位均变为1，而第n位变为0——0～n为与原值相反，n位以上与原值相同。此时将减1后的值与原值取与，可知取与结果的低n+1位必为0。若原值在n位以上仍存在1，则取与结果必不为0，由上段推论知，此时原值必不为2的幂次。若原值在n位以上全0，则取与结果必为0，此时原值必为2的幂次。

显然非正值必不为2的幂次。

int isPower2(int x)
{
    int msk = x + ~0;
    return !(x & msk) & !(x >> 31) & !!x;
}

Puzzle 6 - float_neg

float_neg - Return bit-level equivalent of expression -f for floating point argument f. Both the argument and result are passed as unsigned int’s, but they are to be interpreted as the bit-level representations of single-precision floating point values.
When argument is NaN, return argument.
Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
Max ops: 10
Rating: 2

本题需要对浮点数的构成有基本的了解，鉴于下题需要对浮点数有极为全面的认识，此处建议提前阅读IEEE754与单精度浮点数，注意文章中对NaN的定义并思考相反数的求法。

0x7fffffff = 0111 1111 1111 1111 1111 1111 1111 1111
0x7f800000 = 0111 1111 1000 0000 0000 0000 0000 0000
0x80000000 = 1000 0000 0000 0000 0000 0000 0000 0000

本题只需判断参数uf是否为NaN，是则返回其本身，否则返回其相反数。

制作低31位全1的掩码，同原值取与以保留参数uf除去符号位的值，取与结果同0x7f800000相比可判断原值是否为NaN。

求相反数只需变换符号位，同掩码0x80000000异或即可。

unsigned float_neg(unsigned uf)
{
    int msk = 0x7fffffff;
    unsigned low = uf & msk;
    if (low > 0x7f800000)
        return uf;
    else {
        msk = 0x80000000;
        return uf ^ msk;
    }
}

Puzzle 7 - float_i2f

float_i2f - Return bit-level equivalent of expression (float) x
Result is returned as unsigned int, but it is to be interpreted as the bit-level representation of a single-precision floating point values.
Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
Max ops: 30
Rating: 4

本题需将int型参数x转化为单精度浮点数float型数值，即实现类型转换(float)x的功能。如果你对浮点数没有基本的了解，可能会认为int型x是整数，转化为float型就不存在小数了。为避免类似一些误解，需要对浮点数有极为全面的认识，此处建议提前阅读IEEE754与单精度浮点数。

整数转化为浮点数，首先将整数的二进制编码转化为科学计数法$m\times 2^{e}$的形式，其中$m$的小数部分便对应浮点数的fraction位，$e$对应浮点数的exponent位，符号位互相对应。例如$78=1001110_{2}=1.00111\times 2^{6}_{2}$，故sign位为0，exponent位为$6+127=133=100 00101_{2}$，fraction位为$001 1100 0000 0000 0000 0000$。

由于浮点数由sign、exponent、fraction三部分组成，可以分三部分来进行转换。

Declare Variables

sig、exp、frc分别代表浮点数的三部分；frcMsk为fraction位全1的掩码，用于存放fraction位；eBit指向x中1的最高位。

int sig = (x >> 31) & 1;
int exp, frc;
int frcMsk = 0x7fffff;
int eBit = 1;

Judge Special Value

特殊值只需返回特定值。

当x的值为0x80000000时，即$-2^{31}$，是有符号int型最小值。为避免操作可能导致的溢出错误，此处直接返回其float值，即exponent部分为$31+127=158$，其他位均为0。

if (x == 0)
    return x;
else if (x == 0x80000000)
    return 0xcf000000;

Judge Sign

负数转化为其相反数进行运算。

1 2	if (sig) x = -x;

Get Exponent Bits

当右移eBit位后为0，而右移eBit-1位不为0时，说明eBit-1位1所在最高位。例如$78=1001110_{2}$，右移6位不为0，而右移7位为0，故1所在最高位为第6位。

1
2
3

while (x >> eBit)
    eBit++;
exp = --eBit + 127;

Get Fraction Bits

左移31-eBit位，将1所在最高位移动到第31位。当x为$78=1001110_{2}$时，移动后即$$78=1001 1100 0000 0000 0000 0000 0000 0000_{2}.$$再右移到fraction的位最高位后$$0000 0000 1001 1100 0000 0000 0000 0000$$同掩码$$0000 0000 0111 1111 1111 1111 1111 1111$$取与，即可得到fraction位。

至于为什么将最高位的1舍弃，请返回并继续阅读。

1 2	x = x << (31 - eBit); frc = (x >> 8) & frcMsk;

Round to Even

上面的fraction是将x右移8位后取得的，应该考虑被移出去的8位是否满足进位的条件，若符合应该进行进位。

先取x的低8位，若大于一半或者等于一半，应该进位。注意此处进位为向偶数进位，即若等于一半且被进位的位置为0时不进位。

进位之后fraction位会出现变化，若超出23位长，应向exponent进位，且进位后fraction与掩码取与重置。

x &= 0xff;
if ((x > 0x80) || ((x == 0x80) && (frc & 1)))
    frc++;
if (frc >> 23) {
    exp++;
    frc &= frcMsk;
}

Return Result

将各部分左移到相应位置取或即可。

1	return (sig << 31) \| (exp << 23) \| frc;

Source Code

unsigned float_i2f(int x)
{
    int sig = (x >> 31) & 1;
    int exp, frc;
    int frcMsk = 0x7fffff;
    int eBit = 1;

    if (x == 0)
        return x;
    else if (x == 0x80000000)
        return 0xcf000000;
    else {
        if (sig)
            x = -x;

        while (x >> eBit)
            eBit++;
        exp = --eBit + 127;

        x = x << (31 - eBit);
        frc = (x >> 8) & frcMsk;
        x &= 0xff;
        if ((x > 0x80) || ((x == 0x80) && (frc & 1)))
            frc++;
        if (frc >> 23) {
            exp++;
            frc &= frcMsk;
        }
    }

    return (sig << 31) | (exp << 23) | frc;
}

Puzzle …

同时也要注意代码的规范问题，利用辅助工具可以协助提高代码的质量。

例如，运行./btest以检查函数功能的正确性：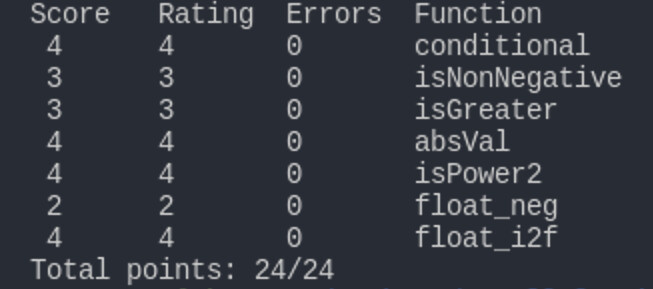
btest2
运行./dlc -e bits.c以检查每个函数的运算符使用情况：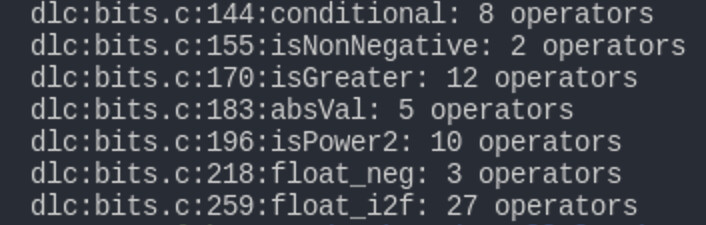
dlc2
运行./driver.pl以同时输出dlc和BDD checker的结果：
driver2